Multiplicacion de polinomios
introducción
INTRODUCCION
La Multiplicación de Polinomios en el 8º Grado de educación básica fue investigada como alternativa multidisciplinaria a presentarse en la exposición técnica de ITEXSAL del año 2008. La cual ha sido preparada, esquematizada y escrita con todo el entusiasmo, responsabilidad y dedicación contribuyendo de esta manera a fortalecer la razón de la visión de nuestra institución ITEXSAL en la vida cotidiana de nosotros los salvadoreños.
En el presente documento nuestra misión es fomentar el conocimiento sobre las bondades que tienen los polinomios y de cómo influye en la vida cotidiana.
El propósito y utilidad del caso de estudio de los polinomios en este documento son los siguientes:
- Conocer en el área de las matemáticas que es la multiplicación de polinomios.
- Fomentar el uso de la multiplicación de polinomios.
- Contribuir al fortalecimiento de las estrategias educacionales sobre las matemáticas en El Salvador.
El I capitulo describe el planteamiento del problema encontrado el cual hace énfasis en la realidad observada sobre el conocimiento que los estudiantes de tercer ciclo tienen sobre polinomios en las ciencias matemáticas.
Luego el capitulo II trata sobre el marco teórico de los polinomios.
Objetivos.
· Reconocer la importancia de la aplicación de la multiplicación de polinomios en las letras y números naturales especialmente en el diario vivir.
· Valorar las propiedades específicas de la multiplicación de polinomios.
· Distinguir problemas más comunes en el procesodel uso de la multiplicación de polinomios en los números naturales en la matemática moderna.
· Demostrar por medio de juegos matemáticos la multiplicación de polinomios, ejemplificarla en una forma divertida, clara y sencilla.
Historia.
Pues, como has podido leer, el padre de Cervantes era “algebrista”.
Esto comienza en el siglo XVI y se desarrolla notablemente en el siglo XVII. Sin embargo, su origen se remonta a los babilónicos y egipcios. En papiros egipcios que datan de 2000 años a. de C. se hallan soluciones de problemas cuya traducción hoy, correspondería a ecuaciones de primer grado.
En el siglo III de nuestra era, el matemático Diofanto de Alejandría escribió la obra Aritmética, en las que crea los signos de la multiplicación, usa abreviaturas y un signo para la sustracción; también resuelve ecuaciones cuadráticas. El aporte de hindúes, árabes y griegos al progreso del algebra es notorio. Comienzan a dar reglas para la solución de ecuaciones de primero y segundo grados con una incógnita.
En el siglo IX, el matemático, astrónomo y geógrafo persa musulmán Abu Abdallah Muḥammad ibn Mūsā al-Jwārizmī (Abu Yā'far) (أبو عبد الله محمد بن موسى الخوارزمي ابو جعفر), conocido generalmente como al-Jwārizmī, vivió aproximadamente entre 780 y 850. Debemos a su nombre y al de su obra principal, Hisab al yabr ua al muqabala, (حساب الجبر و المقابلة) nuestras palabras álgebra, guarismo y algoritmo. La primera palabra significa compensación o restauración (de los dos miembros de la igualdad de una ecuación), y la segunda significa reducción (de términos semejantes).
IX, el matemático, astrónomo y geógrafo persa musulmán Abu Abdallah Muḥammad ibn Mūsā al-Jwārizmī (Abu Yā'far) (أبو عبد الله محمد بن موسى الخوارزمي ابو جعفر), conocido generalmente como al-Jwārizmī, vivió aproximadamente entre 780 y 850. Debemos a su nombre y al de su obra principal, Hisab al yabr ua al muqabala, (حساب الجبر و المقابلة) nuestras palabras álgebra, guarismo y algoritmo. La primera palabra significa compensación o restauración (de los dos miembros de la igualdad de una ecuación), y la segunda significa reducción (de términos semejantes).
 IX, el matemático, astrónomo y geógrafo persa musulmán Abu Abdallah Muḥammad ibn Mūsā al-Jwārizmī (Abu Yā'far) (أبو عبد الله محمد بن موسى الخوارزمي ابو جعفر), conocido generalmente como al-Jwārizmī, vivió aproximadamente entre 780 y 850. Debemos a su nombre y al de su obra principal, Hisab al yabr ua al muqabala, (حساب الجبر و المقابلة) nuestras palabras álgebra, guarismo y algoritmo. La primera palabra significa compensación o restauración (de los dos miembros de la igualdad de una ecuación), y la segunda significa reducción (de términos semejantes).
IX, el matemático, astrónomo y geógrafo persa musulmán Abu Abdallah Muḥammad ibn Mūsā al-Jwārizmī (Abu Yā'far) (أبو عبد الله محمد بن موسى الخوارزمي ابو جعفر), conocido generalmente como al-Jwārizmī, vivió aproximadamente entre 780 y 850. Debemos a su nombre y al de su obra principal, Hisab al yabr ua al muqabala, (حساب الجبر و المقابلة) nuestras palabras álgebra, guarismo y algoritmo. La primera palabra significa compensación o restauración (de los dos miembros de la igualdad de una ecuación), y la segunda significa reducción (de términos semejantes).
El concepto de álgebra de al-Jwārizmī, puede ser comprendido ahora con mayor precisión: se ocupa de la teoría de las ecuaciones lineales y cuadráticas con una sola incógnita, y de la aritmética de binomios y trinomios relativos. La solución tenía que ser general y calculable al mismo tiempo en un sentido matemático, esto es, con un fundamento geométrico. La restricción de grado, así como el bajo número de términos, se explica de manera inmediata. De esta emergencia real, el álgebra puede ser vista como una teoría de las ecuaciones resueltas por medio de radicales1, y de cálculos algebraicos de expresiones relacionadas.
Una parte del libro álgebra de al-Jwārizmī, consiste de aplicaciones y ejemplos. Busca reglas para encontrar el área de figuras como el círculo y también para encontrar el volumen de sólidos, como la esfera, el cono y la pirámide.
El término árabe “al-jarb” se transformó en el castellano “álgebra” y su significado sería restaurar.
Si buscas en un diccionario el significado de la palabra “algebrista” te encontrarás con:
-Persona que se dedica al álgebra (parte de las matemáticas).
-Cirujano dedicado especialmente a la curación de dislocaciones de huesos.
Del escritor e spañol, Miguel de Cervantes de Saavedra, (1547 – 1616), siendo el cuarto hijo de un hombre humilde que según la enciclopedia británica, fue barbero, cirujano y acomodador de huesos es decir “Algebrista”, descubrimos una receta nemotécnica para facilitar la solución a tantas expresiones algebraicas de tercer ciclo básico. Primero debemos romperle los huesos iguales (al muqabala) y luego conciliar el resto de la estructura ósea (al yabr ua) quien describe en el capítulo XV de la obra “El ingenioso hidalgo Don Quijote de la mancha”, parte segunda, aparece el término algebrista en este sentido se narra de cómo Don Quijote vence en buena lid al caballero de los espejos, quien no es otro que su paisano, el bachiller Sansón Carrasco. El bachiller maltrecho y apaleado por el famoso hidalgo, se queja a su escudero de “…el dolor grande de mis costillas…” y concluye este capitulo “…En esto fueron razonados los dos, hasta que llegaron a un pueblo donde fue ventura hallar un algebrista, con quien se curo el Sansón desgraciado…”
spañol, Miguel de Cervantes de Saavedra, (1547 – 1616), siendo el cuarto hijo de un hombre humilde que según la enciclopedia británica, fue barbero, cirujano y acomodador de huesos es decir “Algebrista”, descubrimos una receta nemotécnica para facilitar la solución a tantas expresiones algebraicas de tercer ciclo básico. Primero debemos romperle los huesos iguales (al muqabala) y luego conciliar el resto de la estructura ósea (al yabr ua) quien describe en el capítulo XV de la obra “El ingenioso hidalgo Don Quijote de la mancha”, parte segunda, aparece el término algebrista en este sentido se narra de cómo Don Quijote vence en buena lid al caballero de los espejos, quien no es otro que su paisano, el bachiller Sansón Carrasco. El bachiller maltrecho y apaleado por el famoso hidalgo, se queja a su escudero de “…el dolor grande de mis costillas…” y concluye este capitulo “…En esto fueron razonados los dos, hasta que llegaron a un pueblo donde fue ventura hallar un algebrista, con quien se curo el Sansón desgraciado…”
 spañol, Miguel de Cervantes de Saavedra, (1547 – 1616), siendo el cuarto hijo de un hombre humilde que según la enciclopedia británica, fue barbero, cirujano y acomodador de huesos es decir “Algebrista”, descubrimos una receta nemotécnica para facilitar la solución a tantas expresiones algebraicas de tercer ciclo básico. Primero debemos romperle los huesos iguales (al muqabala) y luego conciliar el resto de la estructura ósea (al yabr ua) quien describe en el capítulo XV de la obra “El ingenioso hidalgo Don Quijote de la mancha”, parte segunda, aparece el término algebrista en este sentido se narra de cómo Don Quijote vence en buena lid al caballero de los espejos, quien no es otro que su paisano, el bachiller Sansón Carrasco. El bachiller maltrecho y apaleado por el famoso hidalgo, se queja a su escudero de “…el dolor grande de mis costillas…” y concluye este capitulo “…En esto fueron razonados los dos, hasta que llegaron a un pueblo donde fue ventura hallar un algebrista, con quien se curo el Sansón desgraciado…”
spañol, Miguel de Cervantes de Saavedra, (1547 – 1616), siendo el cuarto hijo de un hombre humilde que según la enciclopedia británica, fue barbero, cirujano y acomodador de huesos es decir “Algebrista”, descubrimos una receta nemotécnica para facilitar la solución a tantas expresiones algebraicas de tercer ciclo básico. Primero debemos romperle los huesos iguales (al muqabala) y luego conciliar el resto de la estructura ósea (al yabr ua) quien describe en el capítulo XV de la obra “El ingenioso hidalgo Don Quijote de la mancha”, parte segunda, aparece el término algebrista en este sentido se narra de cómo Don Quijote vence en buena lid al caballero de los espejos, quien no es otro que su paisano, el bachiller Sansón Carrasco. El bachiller maltrecho y apaleado por el famoso hidalgo, se queja a su escudero de “…el dolor grande de mis costillas…” y concluye este capitulo “…En esto fueron razonados los dos, hasta que llegaron a un pueblo donde fue ventura hallar un algebrista, con quien se curo el Sansón desgraciado…”
Así, en el siglo XVI, en las puertas de los barberos castellanos había un cartel con la siguiente leyenda: “ALGEBRISTA Y SANGRADOR”. Esto era porque los antiguos barberos además de afeitar también sacaban sangre y restauraban huesos rotos.
Otro tema principal tratado por al-Jwārizmī, en el libro Sindhind zij son los calendarios; el cálculo de las posiciones verdaderas del Sol, la Luna y los planetas, tablas de senos y tangentes; astronomía esférica; tablas astrológicas; cálculos de paralaje2 y de eclipses; y la visibilidad de la Luna. Un manuscrito relacionado, atribuido a al-Jwārizmī, que trata sobre trigonometría esférica
Al-Jwārizmī
, escribió un trabajo importante sobre geografía que daba latitudes y longitudes de 2402 localidades como base para un mapa del mundo. El libro, que está basado en la Geografía de Ptolomeo lista latitudes y longitudes, ciudades, montañas, mares, islas, regiones geográficas y ríos.
Multiplicación de polinomios
Multiplicación de polinomios
- OPCIÓN 1.
- 1Se multiplica cada monomio del primer polinomio por todos los elementos del segundo polinomio.
- 2Se suman los monomios del mismo grado.
- 3Se obtiene otro polinomio cuyo grado es la suma de los grados de los polinomios que se multiplican.
Definición de polinomio
Un polinomio es una expresión algebraica que se obtiene al expresar cualquier suma de monomios no semejantes.
Grado de un polinomio
- Es el grado del término de mayor grado.
- El término de primer grado se llama término lineal.
- El término de grado cero se denomina término independiente.
Multiplicación de un polinomio por un monomio
Sea P(x) un polinomio , y M(x) un monomio, el producto P(x)*M(x) es un polinomio que resulta de multiplicar los coeficientes del polinomio por los del monomio, y sumar a los grados del polinomio el del monomio, si el polinomio es:
y el monomio es:
Podemos Observar Dos Ejemplos De La Multiplicación De Polinomios:
Multiplicar polinomios implica aplicar las reglas de los exponentes y la Propiedad Distributiva para simplificar el producto. Esta multiplicación también puede ilustrarse con un modelo de área y puede ser útil al modelar situaciones del mundo real. Entender los productos de polinomios es un paso importante para factorizar y resolver ecuaciones algebraicas.Otro tipo de multiplicación de polinomios es el producto de un binomio y un trinomio. Aquí también, el proceso es el mismo que con los otros tipos. Cada término en el binomio debe ser multiplicado por cada uno de los términos del trinomio.


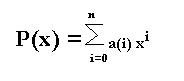
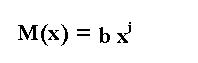

Helen me gusto tu blog esta llamativo mironq el tema que te toco lo supiste acoplar la información y los ejemplos
ResponderBorrarme parece un blog muy interesante hay bastante información pero muy pocos ejemplos.
ResponderBorrarHelen me gusta tu blog muy llamativo esta muy interesante pero casi no miro ejemplos de ejercicios
ResponderBorrarme gusta el diseño, creo que debiste poner ejercicios sobre el tema para que se entendiera más.
ResponderBorrarme gusta el diseño, creo que debiste poner ejercicios sobre el tema para que se entendiera más.
ResponderBorrarmuy buena información me gusto que subió en su blog la historia de donde provenía los múltiplos de polinomios me hubiera gustado que le colocara ejercicios para poderle entender mejor al tema
ResponderBorrarmmm esta muy bonito, es muy llamativo ,le pusistes buena informacion pero creo que te faltaron ejercicios...
ResponderBorrarEsta Bien Tu Blog Helen Y Bonito También Me Gusta El Color Y El Diseño Que Le Pusistes Solo Faltaron Un Poco Mas De Ejemplos
ResponderBorrarme encanta tu blog Helen se ve mucho el desempeño que puso en practica la informacion esta bien pero creo que le faltaron un poco mas de ejercicios es lo unico que le puedo decir
ResponderBorrarBuena información Helen
ResponderBorrarSolo que le falto más ejemplos
Pero muy bonito
Muy creativo
Esta muy bien sólo que hubiese sido mejor si se hubiera explicado más
ResponderBorrarTu blog esta muy bien el diseño y la información solo que le falta mas ejemplos
ResponderBorrarBuen trabajo, me gusto mucho la histora, solo me ubuera gustado ver ejercicios del tema
ResponderBorrarBueno .. esta buena la informacion
ResponderBorrarbuen blog helen muy buena informacion me gusto su diseño
ResponderBorrarbuen trabajo helen buena información solo que debió poner mas ejemplos pero todo lo demás esta bien
ResponderBorrarBuen blog, solo que sobrecargado de informacion que considero innecesaria, ya que hay mas informacion que ejercesios, pero en si buen blog.
ResponderBorrarEsta aceptable pero con ejemplos hubiera sido mejor el blog para entender más sobre el tema.
ResponderBorrarBuen blog, tiene mucha información, pero le faltaron varios ejercicios.
ResponderBorraresta completo de informacion,me gusto la creatividad que de tu diseño
ResponderBorrarle falto ejemplos y seria un poco mas facil entender mejor el tema
buen blog.
Este blogs me pareció excelente so contenido es explendido aunque faltaron algunos ejemplos
ResponderBorrarEJEMPLOS MAS CLAROS DE UN MONOMIO POR UN BINOMIO, DE UN MONOMIO POR UN TRINOMIO, DE UN MONOMIO POR UN POLINOMIO, UN BINOMIO POR UN TRINOMIO, UN BINOMIO POR POLINOMIO, TRINOMIO POR TRINOMIO Y POLINOMIO POR POLINOMIO. EL COLOR NO CONTRASTA CON EL TEMA.
ResponderBorrar